| IODP Proceedings Volume contents Search | ||

|
||
| Expedition reports Research results Supplementary material Drilling maps Expedition bibliography | ||
|
doi:10.2204/iodp.proc.311.108.2006 Tool performanceCalibrationThe prototype APCT-3 tool was made available for use only a few days prior to the start of Expedition 311. Fortunately, there was time for calibration across a limited range of 1.5°–9.5°C. During calibration, the APCT-3 and a calibrated reference thermistor were submerged in a continuously stirred, cylindrical water bath ~60 cm in diameter and ~75 cm high. Calibration bath temperatures were maintained by competing cooling and heating systems controlled using the reference sensor. Temperatures measured with the reference sensor have absolute accuracy of better than 2 mK and were recorded when the temperature in the tank was within a small window around each of five temperature values used for calibration. The limited temperature range of pre-Expedition 311 calibration resulted mainly from limitations in available time. A wider temperature range will be used for calibration of the production APCT-3 tools and prototype during the coming year. There are two general ways to apply calibrations to APCT-3 temperature data. One way is to apply an experimentally determined calibration to the exported ASCII data. Alternatively, one could also create new calibration files (*.wtc) that are used by the WinTemp software. To do the latter, one must supply two pairs of A/D converter readings, x (digital counts), and corresponding resistances R (Ohm) and three pairs of resistances and corresponding reference temperatures T (°C). The x-R pairs are used to identify the scale m and the offset b in the equation R = m(x + b)/(13,1071 – [x + b]), (1)
which is used to compute resistances R from logger readings x. Subsequently, the R-T pairs are used to compute the coefficients Ai in a standard (Steinhart and Hart, 1968; Bennett, 1972) equation: 1/T = A1 + A2In(R) + A3ln3(R). (2)
Note that although WinTemp requires entering reference temperatures in Celsius, computations in Equation E2 are done in Kelvin and R is dimensionless (resistance divided by 1 Figure F4A shows the calibration reference temperatures and respective APCT-3 temperatures, which were computed with the standard WinTemp calibration file. The differences between reference temperature and APCT-3 temperature range from about –37 mK at 1.5°C to –29 mK at 9.5°C (Fig. F4B, F4C). Linearly extrapolated over the whole measurement range from –5° to 55°C, these differences range from –44 to 18 mK, respectively. Using an ad hoc approach, all APCT-3 temperature data shown in the site chapters of the Expedition 311 Proceedings of the Integrated Ocean Drilling Program were corrected by adding a constant offset of 30 mK. This approach is justified because the accuracy of undisturbed formation temperatures extrapolated by the TFit software is on the order of ±0.1°C. To take advantage of the APCT-3's enhanced resolution and accuracy in a new temperature extrapolation algorithm, however, a more sophisticated calibration approach will be developed for future use with the production APCT-3 tools. Reference temperatures and resistances, computed using Equation E1 and the constants b and m provided by Antares, were used to determine optimized coefficients Ai in Equation E2 (see Fig. F4D; Table T1). The resulting standard deviation of the differences between reference temperatures and APCT-3 temperatures of 0.6 mK (Fig. F4E, F4F) is similar to the APCT-3's temperature resolution in the given temperature interval (Fig. F2). Numerous temperature data measured with MTLs testify (e.g., Heesemann et al., 2005) that this excellent signal to noise ratio is typically achieved by the Antares temperature logger electronics. As shown in Figure F5, small temperature undulations in the order of a few mK that occur while a temperature plateau is held in the calibration bath are resolved by the reference thermistor as well as the calibrated APCT-3 temperatures. During rapid temperature changes, there is, however, a small apparent time lag between the APCT-3 temperature and the reference temperature resulting in increased temperature differences. For instance, this behavior causes the increased temperature differences during oscillations at the beginning of the temperature plateaus (cf. Figs. F4B, F5B). The time lag is caused by a somewhat greater response time for the APCT-3 electronics than for the reference sensor. This is not surprising since the APCT-3 tool is placed inside a coring shoe having a large thermal mass, and there is an imperfect contact between the sensor and shoe, with heat sink compound used to fill the gap between the sensor prong and the index hole in the coring shoe. The thermal time constant of the APCT-3 tool in the coring shoe characterizes the response time of the temperature measurement system to an abrupt change in temperature. It is defined as the time that is required until the difference between the sensor temperature and the new ambient temperature is reduced to 1/e (~36.8%) of the initial temperature difference. Typical time constants of glass-encapsulated thermistors in a well-stirred bath are ~1.5 s. During Expedition 311, experiments to estimate the time constant of the APCT-3 cutting shoe were performed. The tool was alternately submerged in containers with cold and warm water (cf. Fig. F6A). As shown in Figure F6B, the three resulting rapid transients were normalized so that the beginning of all transients equals one and all transients approach zero. Because of temperature variations in the containers, the steady-state temperature that is set to zero is not well defined. Nevertheless, it is possible to demonstrate that the APCT-3's time constant is on the order of 10 s. Results from Expedition 311During Expedition 311, nine APCT-3 deployments were performed in depths ranging from ~30 to ~114 meters below seafloor (mbsf). The overall data quality was excellent, and the standard TFit program was applied to all data measured at Sites U1325, U1326, and U1329. The three measurements at Site U1328 could not be processed because the deployments were disturbed by heave resulting from high seas. A complete temperature data set of a typical APCT-3 deployment (Core 311-U1325B-8H; 71.5 mbsf) is shown in Figure F7. Plots of all temperature data obtained during Expedition 311 are provided in their respective site chapters. All important stages of an APCT-3 deployment cause a specific temperature signal, as recorded by the tool. These stages are as follows (numbers refer to parts of the example record in Fig. F7):
Figure F8A compares second-generation APCT data (Core 311-U1329C-11H; 95.6 mbsf) with APCT-3 data (Core 311-U1329C-13H; 114.6 mbsf). The APCT data exhibit a higher temperature peak caused by frictional heating in this example, probably as a result of penetrating sandier sediments, and there is a slower decay toward undisturbed formation temperature. Even though the temperature resolution as well as the time resolution of the APCT-3 surpasses the values of the older APCT by about one order of magnitude, both recorded decay curves appear to be well resolved. The derivative with respect to time of the APCT-3 data (Fig. F8B), however, reveals that temperature changes at the end of the decay curve are on the order of 1 mK/s, matching the resolution of the APCT-3 tool. As shown in Figure F9 a time resolution of 10 s is not sufficient to resolve the temperature changes of the heat pulse generated during the penetration of the probe. Figure F9A–F9C shows one temperature peak measured at a sampling interval of 1 s and three hypothetical measurements of the same data recorded using a sampling interval of 10 s. Whereas time and magnitude of the temperature peak are well resolved in the APCT-3 measurement, the errors in estimated peak time and magnitude of the theoretical APCT measurements (e.g., Fig. F9B) are as much as ~5 s and ~20%, respectively. It should be noted that early-time data (the first 20–60 s) following APCT insertion are typically omitted when estimating equilibrium formation temperatures; therefore, it is not clear whether the lack of temporal resolution common during many earlier deployments resulted in a systematic bias in calculated formation temperatures. Additional analysis of APCT-3 response will be completed as part of the ongoing project, but initial tests with the APCT-3 tool give confidence as to the performance of the new electronics. In order to cross-check the APCT-3 data with other downhole temperature data, we attempted to colocate measurements with the Davis Villinger Temperature Probe (DVTP). Unfortunately, these attempts failed because of bad weather conditions. Nevertheless, APCT-3 data are consistent with temperatures measured with other tools. For instance, the linear vertical temperature profile at Site U1329 (Fig. F10) provides additional qualitative verification of the data quality. Considering a mean thermal conductivity of 1.05 W/(m·K) (Fig. F10B), all estimated undisturbed formation temperatures are consistent with a conductive heat flux of ~72 mW/m2. Furthermore, the extrapolated seafloor temperature of 3.5° ± 0.5°C matches seawater temperatures of 3.5° ± 0.2°C (see the "Site U1329" chapter) at the water depth at Site U1329 (950 m). The seawater temperatures off Vancouver Island were measured within the World Ocean Circulation Experiment (WOCE) in September 1985 (WOCE Section P01) and in February 1994 (WOCE Section PR06). |
||

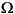 ). This empirical equation is known to provide a good match to thermistor characteristics with a minimum number of free parameters. Figure
). This empirical equation is known to provide a good match to thermistor characteristics with a minimum number of free parameters. Figure